CorticelliBlog

Tavoletta babilonese

Su una tavoletta d’argilla, ritrovata tra le rovine di una città della Mesopotamia e risalente al periodo paleobabilonese della dinastia Hammurabi (1800 – 1600 a. C.), è disegnato un quadrato e le sue diagonali. Su un lato è riportato il numero 30 e su una diagonale i numeri 1,414213… e 42,42639…. Il primo dei due numeri, sulla diagonale, è un valore approssimato, ma già molto preciso, della radice di 2, l’altro è la diagonale del quadrato, cioè il prodotto di 30 per questo numero. Un calcolo che prevede la conoscenza del teorema di Pitagora.

Questa tavoletta, che oggi è conservata negli Stati Uniti, all’Università di Yale, è importantissima. Infatti viene riportata in tutti i testi di storia della matematica come prova del fatto che il teorema di Pitagora era già noto almeno mille anni prima di Pitagora. Vale a dire che il teorema di Pitagora … non è di Pitagora. Se ne trovano tracce in molti altri documenti non solo babilonesi, ma di altre civiltà, ad esempio dell’Antica Cina o dell’India, ben prima della nascita di Pitagora. Se noi siamo portati a privilegiare e a mettere in primo piano la civiltà greca, è soltanto perché questa è alle radici del pensiero della nostra civiltà occidentale.

In generale possiamo dire che è molto difficile, a volte impossibile, risalire all’origine delle idee matematiche. Queste non sono patrimonio di un’unica civiltà e ancora meno di un solo uomo. Per fortuna, a nessuno, finora è venuto in mente di brevettare un teorema, come accade invece regolarmente per i farmaci o i software delle industrie chimiche o informatiche. Le idee della matematica appartengono a tutta l’umanità, nascono spesso nello stesso periodo, in ambienti diversi, e si arricchiscono con il contributo di più persone, a dimostrazione del fatto che la matematica è la vera scienza universale e sicuramente la più democratica. Ne abbiamo una prova proprio con il teorema di Pitagora.

Furono soltanto i pitagorici ad attribuirlo a Pitagora, obbedendo alle loro regole, secondo le quali si doveva attribuire al maestro ogni scoperta, e questo anche dopo la sua morte, perché era sempre lui ad ispirare e guidare qualsiasi lavoro. Il suo merito o più probabilmente di qualcuno dei suoi discepoli, è stato quello di averne dato una dimostrazione rigorosa e più in generale di aver avviato un’analisi approfondita dei principi sui quali si fonda il teorema.

Pitagora e i pitagorici

Pitagora (con questo nome non si indica solo Pitagora ma tutta la sua scuola perché è impossibile distinguere i suoi lavori da quelli dei suoi discepoli) segna il momento di passaggio dalla matematica applicata alla matematica astratta, con l’introduzione di dimostrazioni fondate su un metodo rigoroso (metodo deduttivo) a partire da assiomi ossia a partire da definizioni assunte come vere.

Pitagora nacque a Samo, un’isola della Ionia, nel 580 a. C. Quando aveva circa quarant’anni, dopo essere stato allievo di Talete e dopo aver visitato molti paesi, in particolare l’Egitto e la Babilonia, abbandonò la sua patria per sfuggire alla dittatura di Policrate e si stabilì a Crotone, in Calabria, dove fondò una comunità filosofica e religiosa che si impegnò direttamente nell’attività politica della regione.

Alla fine del sesto secolo, una sommossa, guidata dai nobili locali, cacciò i pitagorici da Crotone. Pitagora si rifugiò a Metaponto dove poco dopo morì. I suoi seguaci crearono in seguito nuove comunità, nel nome del maestro, venerato come un dio. La più celebre fu quella di Taranto. La vita di Pitagora, del quale non è rimasto alcun scritto, diventò ben presto leggenda e non è possibile avere notizie certe su di lui.

Sappiamo che predicava l’astinenza e il digiuno. Credeva nella reincarnazione dell’anima in specie diverse, fino alla loro eventuale purificazione e alla conseguente uscita dalla “ruota delle nascite”. Lo studio della matematica era visto come lo strumento per raggiungere questa liberazione dell’anima dal corpo: numeri e forme della matematica, con la loro bellezza e perfezione, sostenevano i pitagorici, potevano guidare l’anima verso il cielo.

Il rapporto fra numeri e musica, scoperto dai pitagorici, è un esempio del collegamento dei numeri con l’armonia del cosmo. Un famoso matematico circa 600 anni dopo scriveva:: ” Prendeva alcuni vasi tutti uguali e, mentre ne lasciava uno vuoto, riempiva il secondo d’acqua fino a metà, poi li percuoteva entrambi e otteneva il rapporto di un’ottava. Quindi, lasciando ancora vuoto uno dei vasi, riempiva l’altro per una quarta parte, e poi li percuoteva entrambi e otteneva il rapporto di quarta. Il rapporto tra il vuoto di un vaso e quello dell’altro era dunque di 2 a 1 nell’accordo di ottava e di 4 a 3 nell’accordo di quarta.”

I seguaci di Pitagora si dividevano in “ascoltatori” e “matematici”, gli unici che avevano diritto a conoscere gli insegnamenti più profondi del maestro. Chi aspirava ad entrare nella comunità doveva osservare cinque anni di silenzio e in questo periodo di tempo doveva già affidare alla comunità tutti i suoi averi. Fatto eccezionale, anche le donne erano ammesse alle lezioni di Pitagora. La vita dei pitagorici era per certi aspetti quasi monacale, in una comunione dei beni e nell’osservanza di riti e regole molto rigorose che contribuivano a creare attorno alla scuola un alone di rispetto e di mistero.

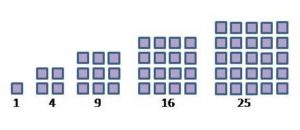
Numeri quadrati

Per i pitagorici “tutto è numero” ovvero ogni cosa può essere ridotta a una relazione numerica. E per i pitagorici i numeri erano soltanto i numeri interi e questi erano il principio di tutte le cose. I numeri assumevano un valore simbolico, che andava oltre la matematica, un valore magico e religioso. Il numero 1 che rappresentava l’Universo non era considerato né pari né dispari ed era considerato il principio di tutti i numeri, come dice Dante nel canto XV del Paradiso. Per i pitagorici il numero 4 era il simbolo della giustizia, essendo il primo numero uguale al prodotto di due numeri uguali, 2 x 2, e anche la giustizia doveva cercare di restituire “l’uguale all’uguale”. Il numero 5 rappresentava il matrimonio, perché somma del primo numero pari (femminile), il 2, con il primo numero dispari (maschile), il 3. E così via, ogni numero con un significato trascendentale. I pitagorici inventarono una singolare teoria, l’aritmogeometria, che collegava fra loro numeri e figure geometriche. Possiamo immaginare che conducessero le loro analisi insieme agli allievi, sulle spiagge di Crotone, usando sassolini bianchi e neri per “costruire” i numeri. Dallo studio di queste figure e dei numeri ad esse collegati si possono ricavare diverse proprietà aritmetiche e geometriche. Ancora oggi usiamo l’espressione “tre al quadrato”. Queste espressioni derivano proprio dalla rappresentazione geometrica dei due numeri: un quadrato di 3 per 3 punti . I numeri “triangolari” formano dei triangoli equilateri e così via.

La leggenda della scoperta del teorema

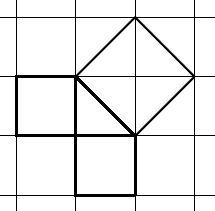
Piastrelle di Pitagora

Si racconta, ma è leggenda, che Pitagora abbia scoperto il suo teorema mentre stava aspettando di essere ricevuto da l dittatore Policrate. Seduto in un grande salone del palazzo del tiranno di Samo, si mise ad osservare le piastrelle quadrate del pavimento. Se avesse tagliato in due una piastrella lungo una diagonale, avrebbe ottenuto due triangoli rettangoli uguali. Inoltre l’area del quadrato costruito sulla diagonale di uno dei due triangoli rettangoli risultava il doppio dell’area di una piastrella. Questo quadrato risultava infatti composto da quattro mezze piastrelle, cioè da due piastrelle (come si può vedere nella figura accanto). Ma i quadrati costruiti sugli altri lati del triangolo corrispondevano ognuno all’area di una piastrella. In altre parole il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui due cateti.

In realtà la storia del teorema è molto più complessa e le sue origini, come abbiamo già detto, risalgono almeno ad un migliaio di anni prima che Pitagora si dedicasse allo studio dei triangoli rettangoli.

Il teorema di Pitagora era noto un tempo come “il ponte degli asini“, il ponte che riusciva a superare soltanto chi dimostrava di possedere sufficienti attitudini per il pensiero astratto e per un metodo deduttivo da applicare a procedimenti matematici quali erano quelli proposti dai pitagorici.

La definizione

L’enunciato del Teorema, che ritroviamo in tutti i testi scolastici e che deriva dalla definizione di Euclide, è il seguente:

In ogni triangolo rettangolo il quadrato dell’ipotenusa (oppure: l’area del quadrato costruito sull’ipotenusa) è equivalente alla somma dei quadrati dei due cateti (oppure: alla somma delle aree dei quadrati costruiti sui due cateti).

Le dimostrazioni

Le dimostrazioni del celebre teorema non sono infinite, ma nel corso dei secoli ne sono state proposte diverse centinaia, con molte varianti, e il loro numero continua a crescere grazie a quelle che ancora oggi vengono scoperte da matematici professionisti o dilettanti, sempre affascinati da questo teorema. Se andiamo a curiosare fra le tante dimostrazioni, ne troviamo alcune veramente curiose.

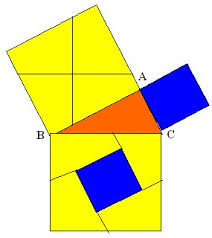
Dimostrazione di Perigal

Nel 1873 da Henry Perigal, un agente di cambio inglese con la passione per la matematica è autore di una delle più famose dimostrazioni. Egli divide il quadrato costruito sul cateto maggiore in quattro parti, con due segmenti passanti per il centro del quadrato stesso, uno dei quali parallelo e l’altro perpendicolare all’ipotenusa, e ricompone poi i quattro pezzi, insieme al quadrato costruito sull’altro cateto, nel quadrato dell’ipotenusa.

Un’altra interessante dimostrazione è quella “poetica” di Airy.   Airy presenta la figura in questo modo: I am, as you can see, When two triangles on me stand, Square of hypothenuse is plann’d. But if I stand on them instead, The squares of both sides are read.

Dimostrazione di Airy

La traduzione: Come potete veder, Io sono qui, Quando i due triangoli sono sopra di me, Si può vedere il quadrato dell’ipotenusa. Se, invece, i due triangoli sono sotto di me, si possono vedere i quadrati dei cateti. questi di sotto invece stanno.

Se osservate la figura a destra, la dimostrazione si ricava facilmente. Il soggetto della poesia è la figura bianca al centro. Quando i due triangoli rossi sono sopra la parte bianca, si può vedere il quadrato dell’ipotenusa (formato dalla parte bianca e dai due triangoli rossi) mentre se i due triangoli blu si trovano sotto alla parte bianca, si formano i due quadrati costruiti sui cateti.

Vediamo ancora la dimostrazione trovata nel 1876 da James A. Garfield, ventesimo presidente degli Stati Uniti. Antischiavista, eroe della guerra civile,

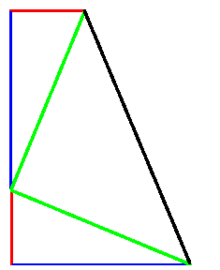
Dimostrazione di Garfield

Garfield venne eletto presidente nel 1880 e avviò subito una campagna contro la corruzione politica, procurandosi per questo molti nemici. Pochi mesi dopo la sua elezione, venne ferito con alcuni colpi di pistola e morì per le scarse condizioni igieniche in cui i medici lo avevano operato. Garfield trovò una dimostrazione inedita del teorema insieme ad alcuni suoi colleghi del Congresso, in un “momento di passatempo matematico”.

“Pensiamo che su questa dimostrazione”, disse, “si possano trovare d’accordo tutti i deputati, indipendentemente dalle loro idee politiche”. La dimostrazione di Garfield, molto bella, si fonda sul calcolo dell’area del trapezio. In questo caso non dobbiamo costruire alcun quadrato. Come si può osservare nella figura, si posizionano vicino due triangoli rettangoli uguali formati dai lati blu, rossi e bianchi). Si unisce, con una retta, due vertici dei triangoli per formare un trapezio. Sia l’altezza che la somma delle basi corrisponde alla somma dei lati blu e di quelli rossi, quindi l’area del trapezio (chiamando x il lato rosso e y il lato blu) è:

Ma l’area dello stesso trapezio è anche uguale alla somma delle aree dei tre triangoli rettangoli della figura. Se chiamiamo il lato verde z,  l’area delle tre figure è:

Uguagliando, otteniamo:

Se si semplifica, si ottiene la relazione del teorema di Pitagora:

x² + y² = z²

Il teorema di Pitagora continua ad essere valido anche se si sostituiscono i triangoli rettangoli con altre figure, ad esempio, triangoli scaleni, pentagoni, esagoni o poligoni irregolari, purché siano sempre figure simili fra loro, conservino cioè la stessa forma e differiscano soltanto per le dimensioni. Il teorema continua ad essere valido per tre semicerchi costruiti sui lati del triangolo rettangolo: l’area del semicerchio costruito sull’ipotenusa è equivalente alla somma dei semicerchi costruiti sui cateti. Da quest’ultima costruzione si arriva a un risultato molto interessante. Se ribaltiamo il semicerchio sull’ipotenusa vale sempre naturalmente la relazione precedente: il semicerchio sull’ipotenusa (ribaltato) è equivalente alla somma dei semicerchi sui cateti.

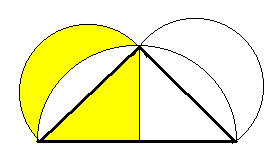
Lunule di Ippocrate

Togliamo poi le parti più scure, sia al semicerchio sull’ipotenusa che ai due semicerchi sui cateti. Rimarranno rispettivamente il triangolo e le due parti più chiare la cui somma risulta equivalente all’area del triangolo, perché differenze di aree uguali. Le due figure chiare a forma di luna, vengono chiamate lunule, piccole lune, dal latino lunulae. Nel caso di un triangolo rettangolo isoscele, una lunula è quindi equivalente alla metà del triangolo. In questo modo risulta che una figura rettilinea, il triangolo rettangolo, ha la stessa area di una figura curvilinea, la lunula. Il primo ad aver dato questa dimostrazione pare che sia stato Ippocrate di Chio, nel quarto secolo a. C.

Le verifiche del teorema

Esistono diversi modi per verificare il teorema di Pitagora.

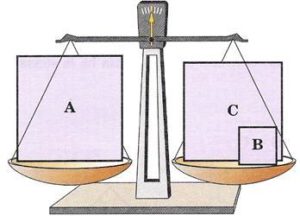
Pitagora con la bilancia

Quadrati di legno e bilancia. E’ necessario costruire tre quadrati di legno (o di cartoncino piuttosto spesso) i cui lati corrispondono a terne pitagoriche. Utilizzando una bilancia si può osservare come il peso dei due quadrati costruiti sui cateti corrisponde al peso del quadrato costruito sull’ipotenusa.

Pitagora e l’acqua

Acqua. Nel video (visibile a questo LINK) possiamo vedere uno strumento formato da un disco con un triangolo rettangolo nel centro. Su ogni lato del triangolo sono stati installati recipienti quadrati. Ruotando il disco, si può osservare che la quantità d’acqua contenuta nel recipiente costruito sopra l’ipotenusa è uguale a quella che possono contenere i recipienti quadrati costruiti sui cateti.

L’altra faccia del teorema di Pitagora

Finora abbiamo parlato dell’aspetto geometrico del teorema, di triangoli rettangoli. Vediamone ora l’aspetto aritmetico, cioè le particolari terne numeriche, chiamate terne pitagoriche, collegate al teorema stesso. Già sappiamo che in un triangolo rettangolo di cateti a, b e di ipotenusa c si ha: a² + b² = c². Esistono infinite terne con numeri interi che soddisfano a questa relazione. Una di queste è 3, 4 e 5. Infatti con questi tre numeri si ha: 3² + 4² = 5². Altre terne sono 5, 12 e 13, 7, 24 e 25, 8, 15 e 17, 20, 21 e 29. Per costruire un triangolo rettangolo è sufficiente costruire un triangolo con le misure dei lati corrispondenti ai numeri di una delle terne pitagoriche, ad esempio di 3, 4 e 5 unità. Lo possiamo verificare praticamente con una scatola di fiammiferi, costruendo un triangolo che abbia come lunghezza dei lati 3, 4 e 5 fiammiferi. Il triangolo ottenuto avrà sicuramente un angolo retto.

Terne pitagoriche

Il collegamento fra il problema aritmetico e il corrispondente problema geometrico, cioè fra e terne pitagoriche e triangolo rettangolo non fu probabilmente così immediato. E’ difficile pensare che il teorema di Pitagora abbia potuto avere origine dalla conoscenza della terna pitagorica 3, 4 e 5.

Una precisa dimostrazione di questo teorema, che possiamo definire l’inverso del teorema di Pitagora si troverà soltanto in Euclide. Nel primo libro dei suoi Elementi, subito dopo il teorema di Pitagora, si trova il teorema inverso:

Se in un triangolo il quadrato di un lato è uguale alla somma dei quadrati dei due lati rimanenti, allora l’angolo contenuto dai due lati rimanenti è retto.