CorticelliBlog

Triangoli

Quanto misura la somma degli angoli di un triangolo?

Costruiamo un triangolo e pieghiamolo come in figura. Cosa si può osservare? Mettendo vicino i tre angoli si ottiene un angolo piatto quindi la somma degli angoli di un triangolo vale 180°

Possiamo arrivare alla stessa conclusione con un altro esperimento: posizioniamo su una tavoletta di legno due chiodi e uniamoli con un elastico. Infiliamo dentro l’elastico un anellino e proviamo a tirarlo. Cosa succede? Otteniamo una famiglia di triangoli isosceli e allontanando il vertice C osserviamo che questo angolo diventa sempre più piccolo e gli altri due tendono a 90°. Se invece abbassiamo l’anellino possiamo vedere che i due angoli alla base si annullano e l’angolo al vertice diventa di 180°. I due casi limite ci indicano che la somma degli angoli vale 180°

Un triangolo può avere due angoli ottusi? E due angoli retti?

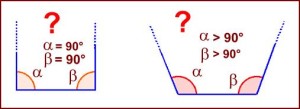
Triangoli rettangoli e ottusangoli

Proviamo ad osservare la figura a sinistra: i due lati che formano con la base due angoli retti nella prima figura e due angoli ottusi nella seconda, non si uniranno mai (nel secondo caso addirittura tendono ad allontanarsi) quindi il triangolo non si potrà mai chiudere. Non può esistere un triangolo con due retti o con due angoli ottusi.

Come si possono classificare i triangoli attraverso gli angoli?

Un triangolo con tre angoli acuti si chiama acutangolo, con due acuti e uno ottuso ottusangolo, con due acuti e uno retto rettangolo.

E attraverso i lati?

Quando i lati sono tutti uguali abbiamo un triangolo equilatero, quando sono uguali almeno due lati abbiamo un triangolo isoscele e quando sono tutti diversi abbiamo un triangolo scaleno.

È possibile combinare le due classificazioni. Il triangolo equilatero è l’unico che sarà sempre acutangolo.

Congruenza dei triangoli

Per capire se due triangoli sono congruenti possiamo ritagliarne uno, spostarlo sull’altro e osservare se tutti i punti coincidono.

Esistono altri metodi?

I principio di uguaglianza

Proviamo a costruire un triangolo utilizzando due lati del meccano e un elastico: se muoviamo i due listelli e quindi l’angolo fra loro, l’elastico si allunga e otteniamo diversi triangoli. Se invece fissiamo l’angolo tra i listelli, il triangolo che si può costruire è unico.

Due triangoli sono congruenti se sono congruenti due lati e l’angolo compreso tra di essi

II principio di uguaglianza

Proviamo a guardare il modello in figura: questa volta rimane fisso un lato e un angolo. Se muoviamo l’elastico si ottengono infiniti triangoli. Se invece fissiamo anche il secondo angolo, il triangolo che si può costruire è unico.

Due triangoli sono congruenti se sono congruenti un lato e i due angoli adiacenti

III principio di uguaglianza

Proviamo a costruire, insieme ad alcuni amici, un triangolo con le striscioline lunghe 6, 7 e 10 cm: i triangoli che ognuno ha costruito hanno la stessa forma.

Due triangoli sono congruenti se i lati sono congruenti

Dal quadrato al rombo

Prendiamo quattro striscioline di carta della stessa lunghezza e uniamole. Che figura otteniamo? Si ottiene una figura articolabile o meglio un insieme infinito di rombi tra cui uno particolare con quattro angoli retti, il quadrato.

Il quadrato è un particolare rombo mentre i rombi non sono tutti quadrati.

Disponiamo le striscioline precedenti in modo da formare il quadrato e facciamo una pressione su un lato per ottenere un rombo: la nuova figura ha lo stesso perimetro?

Proviamo ad analizzare l’area: il rombo diventa più lungo ma più stretto. L’area che perdiamo in altezza la recuperiamo in lunghezza?

Per rispondere osserviamo una figura “limite”: se continuiamo a schiacciare il quadrato otteniamo un rombo sempre più stretto fino a quando la sua area tende a zero.

Tra tutti i rombi isoperimetrici (con lo stesso perimetro), il quadrato è quello con l’area maggiore.

Analizziamo ora quello che succede alla somma degli angoli: il quadrato ha quattro angoli di 90° (quindi la somma è 360°), cosa succede se facciamo una pressione su un lato del quadrato?

Due angoli diventano più grandi quindi maggiori di 90° mentre gli altri due diventano più piccoli. Quello che si guadagna nei primi due si perde con gli altri?

Osserviamo la figura limite: quando arriviamo al rombo più stretto possiamo vedere che due angoli tendono a zero mentre gli altri due sembrano diventare piatti ossia di 180°, quindi in tutti i quadrilateri la somma degli angoli rimane costante e vale 360°.

Cosa succede alle diagonali? Passando dal quadrato al rombo una diagonale aumenta e un’altra diminuisce. Cosa succede alla loro somma?

Nel quadrato ogni diagonale è maggiore di un lato per cui la somma delle diagonali è maggiore della somma di due lati. Quando schiacciamo il quadrato e arriviamo al rombo più stretto osserviamo che una diagonale scompare e un’altra sembra coincidere con due lati allineati quindi con la somma dei due lati.

Quindi la somma delle diagonali è più grande nel quadrato rispetto a quella che ha il rombo con lo stesso perimetro.

Dal rettangolo al parallelogramma

Ora proviamo a costruire un rettangolo con quattro striscioline di carta: il rettangolo ha i lati uguali a due a due e quattro angoli retti. Spingiamo su un lato ed osserviamo cosa succede. Si riesce ad ottenere una famiglia di parallelogrammi tra cui uno particolare con quattro angoli retti, il rettangolo.

Il rettangolo, quindi, è un parallelogramma mentre i parallelogrammi non sono tutti rettangoli.

Tra tutti i parallelogrammi qual è quello con l’area più grande?

Cosa succede alla somma degli angoli passando dal rettangolo al parallelogramma?

Cosa succede alla somma delle diagonali?

Si può rispondere a queste domande utilizzando lo stesso ragionamento che abbiamo usato studiando il passaggio dal quadrato al rombo.

Dal rettangolo al quadrato

Prendiamo due striscioline di carta uguali, foriamole agli estremi e al centro e uniamole con un fermacampione attraverso il foro centrale. A questo punto facciamo passare un elastico nei quattro fori situati alle estremità delle due striscioline. Divarichiamo le striscioline, che figure otteniamo?

Otteniamo un insieme di rettangoli e una figura particolare, il quadrato.

Quali sono gli angoli tra le diagonali quando otteniamo il quadrato? Osserviamo un quadrato solo quando le due diagonali uguali sono perpendicolari fra loro.

Riusciamo ad ottenere un parallelogramma che non sia un rettangolo? No, non è possibile perché parallelogrammi che non sono rettangoli hanno le diagonali diverse.

I rettangoli di filo elastico che otteniamo nella trasformazione da quadrato a rettangolo hanno tutti lo stesso perimetro? No. Esiste una figura con il perimetro minimo? È il quadrato e si può notare che l’elastico ha la tensione minima.

Quadrato e rettangolo hanno una caratteristica comune: le due diagonali uguali

Ogni quadrato è un rettangolo mentre i rettangoli non sono tutti quadrati.

Dal rombo al parallelogramma

Prendiamo due striscioline di carta di lunghezza diversa, foriamole agli estremi e al centro e uniamole con un fermacampione attraverso il foro centrale. A questo punto facciamo passare un elastico nei quattro fori situati alle estremità delle striscioline. Divaricando le striscioline che figure otteniamo? Si ottiene un insieme di parallelogrammi e uno in particolare, il rombo. Osserviamo un rombo solo quando le due diagonali sono perpendicolari.

Riusciamo ad ottenere un quadrato? Non è possibile perché i rombi che non sono quadrati hanno le diagonali diverse.

Anche in questo caso esiste una figura con il perimetro minimo? È il rombo e si può notare che l’elastico ha la tensione minima.

Ogni rombo è un parallelogramma mentre i parallelogrammi non sono tutti rettangoli.

Il trapezio

Prendiamo quattro striscioline di carta lunghe 16, 8, 4 e 4 cm, riusciamo a costruire un trapezio?

Come deve essere la lunghezza della base maggiore rispetto alla somma degli altri tre?

In questo caso il trapezio “non si chiude” perché un lato deve essere più lungo rispetto alla somma degli altri.

Un trapezio è un quadrilatero con due lati paralleli.

Quindi un parallelogramma è un trapezio particolare mentre i trapezi non sono tutti parallelogrammi.

Esistono tre tipi di trapezi: isoscele con due lati uguali e gli angoli uguali due a due, rettangolo con due angoli retti e scaleno con tutti i lati e gli angoli diversi.

Poligoni

Possiamo dividere i poligoni in:

convessi quando la retta che contiene ogni lato lascia il poligono da una parte

concavi quando la retta che contiene un lato taglia il poligono

intrecciati quando almeno due lati si tagliano.

Prendiamo quattro striscioline di carta uguali e uniamole, è sempre possibile costruire un poligono intrecciato?

Si può ottenere un poligono concavo articolando un quadrato, un trapezio o comunque un poligono convesso?

Poligoni regolari

Un poligono è regolare se ha tutti i lati e tutti gli angoli uguali.

Il rombo ha quattro lati uguali. È un poligono regolare?

Il rettangolo ha quattro angoli uguali. È un poligono regolare?

Costruiamo con cinque striscioline di carta della stessa lunghezza, ad esempio 8 cm, un pentagono regolare.

Articolando la figura si possono ottenere pentagoni non regolari? Si può ottenere un parallelogramma? E un trapezio? E un rettangolo? Se si riesce ad ottenere un triangolo, di che tipo è?

Costruiamo con sei striscioline di carta della stessa lunghezza, ad esempio di 8 cm, un esagono regolare.

Articolando la figura, si possono ottenere esagoni non regolari? Parallelogrammi? Trapezi? Rettangoli? Che tipo di triangoli si riesce ad ottenere?